Stiskanje slik s postopkom JPEG
Človeško oko lahko razlikuje svetlost slike bolj natančno, kot njene barvne informacije (pri nizki svetlobi sliko dejansko vidimo v črno-belih barvnih odtenkih, ker je osvetlitev preveč medla, da bi spodbudila čepnice v mrežnici). To pomeni, da mora biti vrednost svetlosti predstavljena veliko bolj natančno, kot dve komponenti barvitosti. Postopek JPEG izkorišča očesno neravnovesje z zmanjševanjem vrednosti barvitosti.
Zmanjšanje vzorčenja (ang. Downsampling) je preprosto proces zmanjševanja vrednosti barvitosti za določen faktor (in je zato prvi korak pri izgubi informacij). Pri formatu JPEG obstajajo trije sprejemljive možnosti: brez zmanjšanja vzorčenja, zmanjšanje vzorčenja z deljenjem vodoravnih vrednosti barvitosti na pol, ali pa zmanjšanje vzorčenja z deljenjem vodoravnih in navpičnih vrednosti barvitosti na pol.
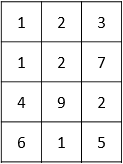
Naslednji korak je razdelitev pikslov na sliki v bloke velikosti 8×8 (ki si jih lahko predstavljamo tudi kot matrike velikosti 8×8). Vsako barvno komponento razdelimo ločeno, vzorec vsake komponente pa gre skozi isti proces, ki sledi v nadaljevanju. Upoštevati moramo, da velikost slike večinoma ne bo preprost večkratnik števila osem pikslov v katerikoli smeri. To lahko privede do nastanka nekaterih neobičajnih pikslov vzdolž desne in spodnje strani slike JPEG.
Vsak blok 8×8 pikslov slike JPEG lahko ustvarimo s seštevanjem različnih količin do največ 64 vzorcev, ki temeljijo na kosinusnih valovanjih. Valovanja lahko vizualno predstavimo kot vzorce belih in črnih pikslov, kot je prikazano na spodnji sliki.

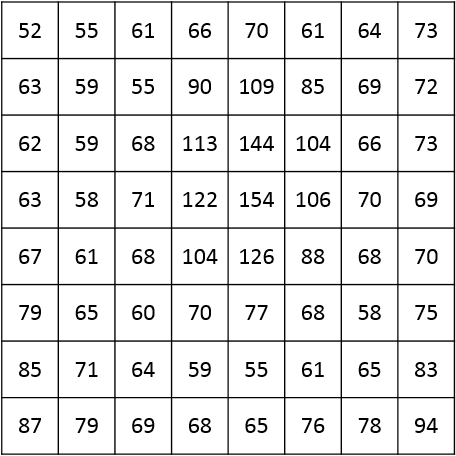
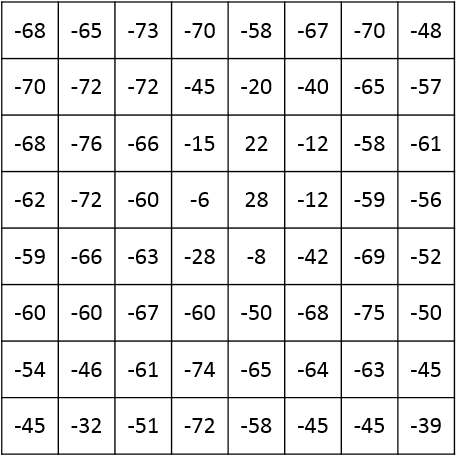
Naslednji korak je zabaven, vendar zapleten. Vsak blok 8×8 z uporabo diskretne kosinusne transformacije (ang. Discrete Cosine Transform – DCT) pretvorimo v drugo matriko. Ta transformacija analizira frekvence prvotnih vrednosti po vsaki vrstici in stolpcu z uporabo množice kosinusnih valovanj, ki nihajo pri različnih frekvencah in amplitudah.
Razlog za to je, da se lahko višje frekvence minimizirajo ali izničijo, ker izgub teh frekvenc ne zaznamo toliko skrajno, kot bi zaznali izgubo bolj energičnih nižjih frekvenc.
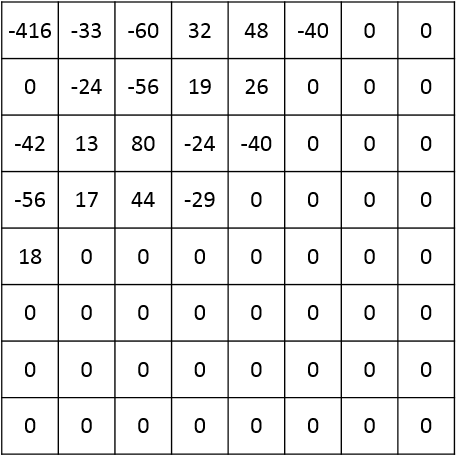
Zanimiva stvar pri tej transformaciji je, da se vrednost z največjo amplitudo nahaja v zgornji levi celici matrike (imenujemo jo tudi DC koeficient), vrednosti pa so tem manjše, čim bolj so oddaljene od te celice (vseh 63 drugih vrednosti, ki jih imenujemo tudi AC koeficienti). V splošnem, za predstavitev vrednosti v tej preoblikovani matriki, potrebujemo več bitov, kot jih lahko shranimo v bajtu (kar smo uporabljali do sedaj).
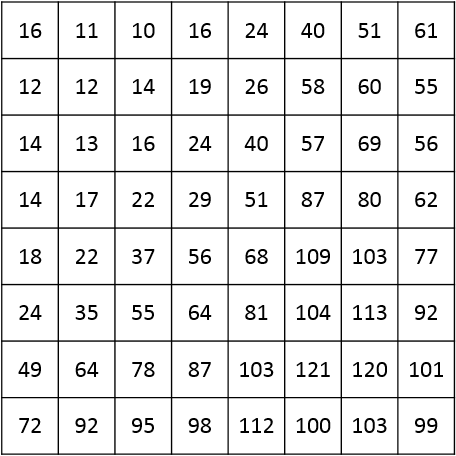
To pretvorjeno matriko v naslednjem koraku nato kvantiziramo. To je glavni del postopka, kjer pride do izgub in faza, kjer minimizirmo višje frekvence nad nižjimi frekvencami. Eden glavnih rezultatov kvantizacije je, da se številni višji DCT koeficienti izničijo, zaradi česar so v naslednjem koraku izredno stisljivi.
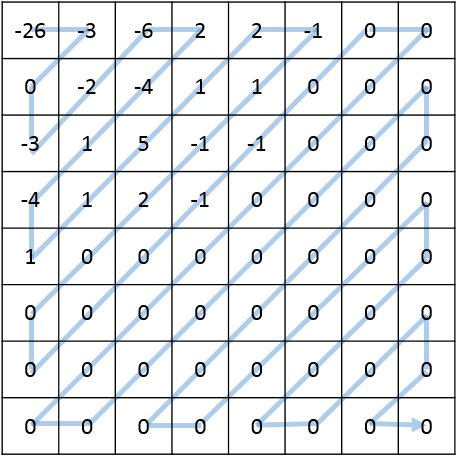
Kvantizacijo dosežemo z množico matrik 8×8, pri čemer vsaka predstavlja drugačen »faktor kakovosti« slike JPEG. Vrednost vsake celice delimo z ustrezno vrednostjo celice v kvantizacijski matriki in rezultat zaokrožimo (ponovno operacija z izgubo). Upoštevati je potrebno, da to ne vključuje množenja matrik v matematičnem smislu.
Končno, dobljena kvantizirano matriko kodiramo s pomočjo Huffmanovega stiskanja. Da bi čim bolj izkoristili dejstvo, da vrednosti matrike padajo iz zgornjega levega kota, vrednosti ne kodiramo po vrsticah, temveč v cikcakastem vzorcu. To pomeni, da se celice z vrednostjo nič ponavadi pojavijo na koncu cikcakaste verige in jih lahko močno stisnemo (v resnici obstaja posebna koda, ki označuje, da so vrednosti vseh preostalih celic v bloku 8×8 enake nič).
Huffmanovo kodiranje je postopek stiskanja brez izgub. Ne pozabimo, da bomo za vsak blok 8×8 pikslov v izvirni sliki (192 bajtov informacij) dobili tri stisnjene, kvantizirane matrike, velikosti 8×8, pri čemer bosta matriki Cr in Cb najbolj stisnjeni.
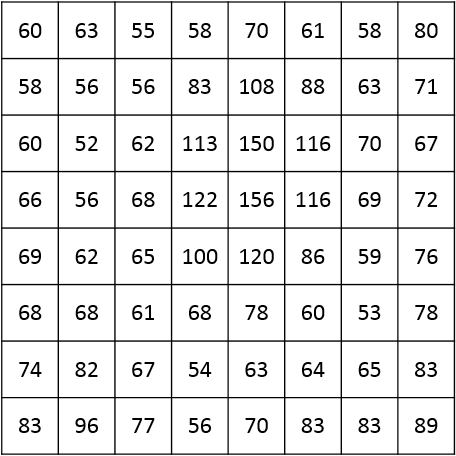
Kako po vsem tem razširimo sliko JPEG v rastrsko bitno sliko, ki jo prikažemo na zaslonu? Precej očitno je, da moramo vse korake opraviti v obratnem vrstnem redu. Najprej moramo odkodirati Huffmanove stisnjene blok 8×8. Tako dobimo kvantizirano matriko. Zdaj lahko količinsko kvantizirano matriko pomnožimo z ustrezno kvantizacijsko matriko, da dobimo matriko DCT koeficientov. To nato spremenimo z inverznim postopkom DCT, da dobimo matriko izvornih komponent v barvnem prostoru YCbCr.
Vsako množico treh komponentnih iz matrike lahko pretvorimo v barvni prostor RGB z uporabo inverznih enačb za pretvarjanje barv. Slika bo zdaj razširjena in pripravljena za prikaz.
Za radovedne
S klikom na ustrezni gumb si lahko ogledaš bolj podrobno razlago delovanja postopka stiskanja in razširjanja slike JPEG. Razlaga je podkrepljena z matematičnimi pojmi na praktičnem primeru.